전기화학 전지의 전해질은 이온 전도를 담당한다. 모든 전해질에서 이온 전도를 위한 이온의 이동은 반드시 일어나야 한다. 전지의 전해질이 수용액인 경우가 많으므로, 수용액에 존재하는 이온 이동 현상을 다룬다. 수용액의 이온은 용매인 물 분자와 이온-용매 상호 작용을. 그리고 다른 이온들과 이온-이온 상호작용을 한다. 그 상호 작용을 이해하면 수용액에 존재하는 이온의 상태를 알 수 있다. 수용액 속 이온은 농도 차이에 의하여 확산(diffusion)하며, 전위 차이에 의하여 전기장 이동(migration)한다. 이온 이동을 설명하는 가장 기본적인 물리량은 이온의 이동도(mobility)이다. 그러므로 확산과 전기장 이동을 설명하는 이론은 ion mobility의 미시적 해석에 초점을 둔다. ion mobility와 연관하여 이온 이동에 수반되는 다양한 전기화학적 현상도 소개한다.
<전기의 이해>
전하 +q의 중심 전하(central charge)를 향해 전하 q’의 시험 전하가 전급하고 있는 상황을 가정한다. 두 전하의 부호가 같으면 반발력이 작용하고, 반대이면 인력이 작용한다. 두 전하 사이의 거리가 r일 때, 두 전하 사이의 전기힘 F는 다음과 같다.

한편 q와 q’의 거리가 r일 때, 두 전하의 퍼텐셜 에너지 U는 q’(시험 전하)이 거리 ∞에서 거리 r까지 이동하면서 외부에 하는 일로 정의되며 다음과 같이 표현된다.

그러므로 두 전하의 부호가 같으면 U>0이므로 묶이지 않은 계가 되고, 반대이면 U<0이므로 묶인 계 가 된다.
퍼텐셜 에너지 U를 보는 관점은 두 가지이다.
시험 전하 q’의 양과 부호가 변화는 관점에서 보자. U를 시험 전하로 미분하면 다음과 같다.

𝚿는 중심 전하 q와 거리 r이 일정한 상황에서 q’에 따른 U의 변화 비율이다. 전하량이 +1C인 시험 전하 q’의 퍼텐셜 에너지, 즉 단위 전하량에 대한 퍼텐셜 에너지를 전기 퍼텐셜(electrical potential) 𝚿 로 정의한다.
양이온 A+와 B+가 r이라는 거리에 떨어져 있는 고체 결정에서 B+ 이온이 B2+이온으로 산화되는 화 학적인 예를 생각해 보자. q’이 +1e에서 +2e로 전하가 증가하였으므로 U는 산화과정에서 증가한다. ∆q’ = +e이므로 증가한 ∆U는 +eΨ이다. 그러므로 전위 Ψ는 시험 전하 변화량에 따른 퍼텐셜 에너지 변화를 결정하는 물리량이다.
시험전하 q’이 이동하여 거리 r이 변화하는 관점에서 보자. 전위를 r에 대해서 미분하면 아래와 같다.

위의 식은 이동 전하가 이동할 때, 전위의 변위를 의미한다. 이는 시험전하 q’이 받는 전기적 힘 F를 의미한다. 중심 전하 q가 있으면 q는 E라는 전기장을 만들어 내고, 시험 전하 q’은 전기장에서 전기힘을 받아 공간에서 이동한다. q와 q’의 부호가 같으면 척력이 작용하여 거리 r이 증가하므로 q’은 전위가 감소하는 방향으로 이동한다. 반대로 q와 q’의 부호가 다르면 인력이 작용하여 거리 r이 감소하므로 q’은 전위가 감소하는 방향으로 이동한다.
지금까지 논의한 물리 법칙과 전기화학을 연결할 필요가 있다. 물리에서 전기와 관련된 기준 q는 +1C의 양전하이다. 전기화학의 산화/환원 반응은 q’를 변화시켜 전위를 변화시킨다. 한편 전위의 공간적 차이에 다른 이온의 이동은 전해질의 이온 전도를 설명한다. 그러므로 전기화학적으로 반응하는 물질과 이동하는 이온의 전기 퍼텐셜 에너지는 변화한다.
전기화학의 논의 과정에 전기적 용어와 화학적 용어가 혼재되어 사용된다. 그러나 혼용되는 용어는 개념적으로 동일하지만 표현에서 차이가 있다. 전기에서는 전하가 주된 관심사이지만, 화학에서는 물질의 상태와양이 주된 관심사이다. 그러므로 전기에서는 전하의 양과 부호가 전기 퍼텐셜 에너지를 결정하지만, 화학에서는 물질의 농도와 상태가 화학 퍼텐셜 에너지를 결정한다.

<2.1 이온-용매 상호 작용: Born 모델>
이온성 고체가 용매에 용해되는 과정에서 고체 결정의 이온은 분산하고 용매 분자에 의하여 둘러싸인다. 특히 수용액의 극성 물 분자가 이온을 둘러싸는 hydration 과정에서 이온의 에너지가 낮아진다. 수화 과정은 이온-용매 상호작용(ion-solvent interaction)이라고 한다.
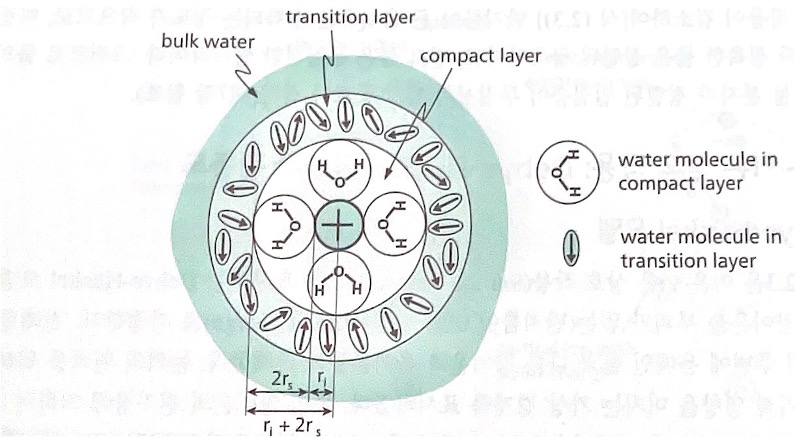
아래 그림은 Born 모델을 보완한 그림이다. 물 분자는 쌍극자이며, 양이온과 접촉하고 있는 물 분자의 이온-쌍극자 상호작용은 매우 강하다. 양이온 근처의 물 분자는 compact layer를 형성하여 이온과 함께 이동할 정도로 그 상호작용은 강하다. 밀접층과 벌크 물의 중간에는 양이온의 전기장에 적게 영향을 받는 transition layer가 존재한다. Bohn 모델의 이온 반지름은 결정 이온 반지름이다. 그러나 수용액의 이온 반지름은 compact layer의 두께(2rs: 물 분자의 크기)도 고려해야 하므로 r + 2rs가 실효 반지름이 된다. 한편 이온 반지름이 큰 경우 이온-물 상호작용이 감소하여 반지름이 큰 음이온은 수화되는 정도가 작아진다. 이온과 접촉한 물은 정렬된 dipole이고, 벌크 물은 무질서한 dipole이다. 그러므로 물의 비유전 상수는 물 분자가 정렬된 밀집층이 무질서한 벌크 물보다 작다.
<2.2이온-이온 상호작용: Debye-Huckel 모델과 활동도>
[Debye-Huckel Model]
그림은 이온-이온 상호작용을 묘사하는 Debye-Huckel 모델이다. +ze의 중심 양이온을 부피가 없는(반지름이 0인) 점전하로 가정한다. 전해질에서 중심 양이온의 주변에 용매인 물과 다른 양이온과 음이온들이 존재한다. 점선으로 표신 원이 중심 이온이 전기적 영향을 미치는 가상 경계이다. 중심 양이온의 전기장에 의하여 음이온은 가상 경계 안으로 끌려오고, 양이온은 가상 경계 밖으로 밀려난다. 가상 경계 내부를 이온 분위기(ionic atmosphere)라고 한다. 따라서 음이온 농도는 이온 분위기 밖보다 높고, 양이온 농도는 그 반대이다.
이온 분위기가 충족해야 하는 조건은 전기적 중성이다. 이온 분위기 안에 있는 모든 이온의 전하 총합은 -ze가 되어야 중심 양이온 전하+ze와 전기적 중성을 유지할 수 있다. 이 조건이 충족된 상황에서 중심 양이온 전하 +ze와 이온 분위기 전하 -ze 사이에 전기적 인력이 작용한다. 이것이 이온-이온 상호 작용의 핵심이다.

이온-이온 상호작용의 에너지를 계산하기 위해서는 이온 분위기 내의 전하 분포를 알아야 한다. 이론 적 접근을 위하여 이온 분위기 안의 이온들은 -ze의 전하가 연속적으로 퍼져 있는 전하구름(charge cloud)으로, 용매인 물은 비유전 상수 𝜀_s인 연속 매질로 가정한다. 복잡한 수학적 유도 과정을 거쳐 중 심 양이온이 이온 분위기를 형성하는 과정에서 한 일(W)은 희석 용액에서 다음과 같다.

rD는 아래에서 자세히 설명할 Debye-length이다. 음의 값을 가지는 W는 중심 양이온의 전하 +ze와 이
온 분위기의 음전하 -ze 사이에 인력이 작용하여 중심 양이온을 포함한 이온 분위기의 퍼텐셜 에어지
감소를 의미한다. (NA/2)는 상호 작용의 중복 계산을 피하기 위해서이며, 𝜀1는 이온 분위기 형성 과정에
서 용매의 역할을 한다. 𝑟 는 중심 양이온 전하 +ze와 이온 분위기 전하 -ze 사이의 평균 거리를 의미 2
한다.
아래의 그림은 중심 양이온으로부터 거리 rD에서 이온 분위기의 전하 밀도가 가장 높음을 예시한다. 이 를 다시 표현하면 (b)와 같이 반지름 rD의 구 표면에 -ze 전하가 위치하는 것과 같다.

𝑰는 용액의 이온 세기(ionic strength)라고 한다. 용액의 농도가 높아지면, 이온의 수가 많아져 이온 분 위기 안으로 유입되는 음이온의 수는 증가하여 중심 양이온과 이온 분위기 안의 이온들 사이의 상호 작용이 증가하여 rD는 감소한다.(𝑟2 ∝ 𝐶3) 한편 이온의 zi가 증가하면 중심 이온과 이온 분위기 안 이온 들 사이의 상호작이 증가하여 rD는 감소한다.(𝑟2 ∝ 𝑧3) 따라서 Debye length에 영향을 줄 수 있는 용액 의 구성 성분과 농도를 표현하는 것이 이온세기이며, Debye length는 𝐼^-1/2에 비례함을 기억한다. Debye-Huckel model은 이온-이온 상호작용을 통하여 중심 이온의 퍼텐셜 에너지 감소를 예측한다. 중심 이온의 전기 퍼텐셜(𝚿) 감소는 용액의 화학 퍼텐셜(𝝁) 감소로 나타난다. 그러므로 Debye-Huckel model의 전기 퍼텐셜과 화학 퍼텐셜을 비교할 필요가 있다.
[화학 퍼텐셜과 활동도]
어떤 물질 X의 수용액의 화학 퍼텐셜 𝜇를 X의 농도가 결정한다. 화학 퍼텐셜을 농도로 표시하면 다음과 같다.
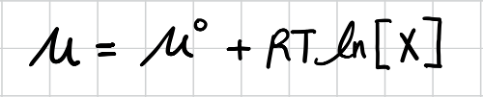
𝜇°는 X의 standard chemical potential이다. 비전해질 X를 먼저 생각해 보자. 농도가 낮으면 분산된 분 자 사이의 거리가 멀어 분산된 분자 사이의 상호작용은 없다. 그러나 농도가 증가하면 용질 분자 사이 의 쌍극자-쌍극자 또는 분산력 등의 상호작용이 있을 수 있다. 그러므로 낮은 농도의 비전해질 용액에 서 분자 간 상호 작용을 무시할 수 있다.
그러나 X가 전해질이면 상황은 다르다. 전해질에 이온이 존재하게 되고 이온 사이에 정전기적 인력이 라는 상호작용이 존재한다. 따라서 아무리 낮은 농도의 전해질이라고 해도 위의 식을 적용하여 chemical potential을 계산해서는 안된다.
전해질에서 이온-이온 상호작용의 크기 ∆𝜇는 상호작용이 없는 이상 용액(ideal solution)과 상호 작용이 있는 실제 용액(real solution)의 화학 퍼텐셜 차이이다. 이상 용액의 화학 퍼텐셜에서는 형식 농도 C(formal concentration)이 들어가고, 실제 용액의 화학 퍼텐셜에서는 활동도 A(activity)가 들어간다. A = fC로 표현하고, f는 활동도 계수이다. 이온-이온 상호작용의 크기 ∆𝜇는 활동도 계수 f로 다음과 같이 표현된다.

따라서, 전해질에서 어떤 이온의 활동도 계수1를 측정하면 그 이온의 ∆𝝁를 실험적으로 측정하는 것이 고 이는 중심 양이온이 이온 분위기를 형성하는 과정에서 한일 W와 동일한 값이다.

∆𝜇를 조금 더 쉽게 설명하면, 어떤 화학 종이 용매에 용해되거나 다른 상태로 변할 때 발생하는 자유 에너지 변화이다. 이 경우, 이온이 용매에 용해될 때의 자유 에너지 변화를 의미한다. 전해질 용액에서 특정 이온의 활동도 계수(f)를 측정하는 것은, 실질적으로 그 이온이 용액 내에서 가지는 화학 퍼텐셜 의 변화를 실험적으로 측정하는 것이다. 이는 해당 이온이 용액 내에서 얼마나 '효과적으로' 존재하는 지를 나타내며, 이는 자유 에너지 변화(∆μ)와 직접적으로 관련된다. 이온이 용액 내에서 중심이 되어 주위에 이온 분위기를 형성할 때, 전기적 상호작용으로 인해 에너지 변화가 발생한다. 이는 양이온이 음이온들과 상호작용하여 안정화되는 과정에서의 에너지 변화를 의미하고, 이 과정에서의 에너지 변화 가 일(W)로 표현될 수 있다. 따라서 특정 이온의 활동도 계수를 측정하여 ∆μ를 구하는 것은, 그 이온 이 이온 분위기를 형성하면서 하는 일(W)을 측정하는 것과 동일한 의미를 가지게 된다. 왜냐하면 결국 ∆μ와 W 모두 이온-이온 상호작용을 계산하는 것이기 때문이다.
-
A=fC->실질적인 농도를 표현하기 위해 f 도입
1) 입자들의 인력작용↑: 실질적인 농도 감소 -> f<1
2) 입자들의 인력작용↓: 실질적인 농도 증가 -> f>1
황동도 계수는 용액 내에서 용질 입자들 사이의 상호작용을 나타내는 값이다. 이상용액에서는 용질 입자들 사이 에 상호작용이 없어 활동도 계수가 1이되지만. 실제 용액에서는 용질 입자들 사이에 인력이나 척력 등의 상호작 용이 존재하기 때문에 활동도 계수는 1과 다른 값을 갖게 된다.
'Electrochemistry' 카테고리의 다른 글
| [Electrochemistry] 전지 전해질과 이온 이동(3) (0) | 2024.08.30 |
|---|---|
| [Electrochemistry] 전지 전해질과 이온 이동(2) (0) | 2024.08.30 |
| [Electrochemistry] 전기화학의 전지(3) (0) | 2024.08.15 |
| [Electrochemistry] 전기화학의 전지(2) (0) | 2024.08.15 |
| [Electrochemistry] 전기화학의 전지(1) (0) | 2024.08.10 |